[４]　２変量間の関係


　　[4.1] 共分散と相関係数
　　[4.2] 散布図
　　[4.3] 相関行列、散布図行列
　　[4.4] 相関係数と範囲の効果

[4.1] 共分散と相関係数

２つの連続変量の関係を表す尺度として、ピアソンの積率相関係数(correlative coefficient)があります。相関係数ｒは、共分散を、ＸとＹの標準偏差の積で割った値です。共分散(covariance)は、Ｘの偏差とＹの偏差の積の総和です。
共分散と相関係数の値を公式通りに算出することもできますが、よく使うので、関数が用意されています。

cov( 変量1, 変量2 )　　　　　　　# 共分散
cor( 変量1, 変量2 )　　　　　　　# 相関係数

[4.2] 散布図

4.2.1 散布図とオプション指定

２変量Ｘ、Ｙの値をＸ軸、Ｙ軸にプロットしたグラフを散布図(scatter plot)と言います。Ｒで散布図を描くには、２変量を指定するだけです。変量１がＸ軸、変量２がＹ軸となります。
plot( ) には、目的に応じて、データ点の形、色など、さまざまなオプション指定が可能となっています。

plot( 変量1, 変量2 )　　　　　# 散布図を描く
オプション col="色名"　　　　 # 色名を英語または数字で指定。デフォルトは1("black")
　　　　　 pch=数字　　　　　 # pch="文字"を指定することも可
　　　　　 cex=数値　　　　　 # 表示サイズ（デフォルトの半分なら0.5)

主な色指定表示色主な形指定表示形
col=1, col="black"黒pch=1○
col=2, col="red"赤pch=2△
col=3, col="green"緑pch=3＋
col=4, col="blue"青pch=4×
col=5, col="aqua"水色pch=5◇
col=6, col="pink"桃色pch=6▽
col=7, col="yellow"黄色pch=16●
col=8, col="grey"灰色pch=17▲

通常は、グラフ画面に１つのグラフが描画されるようになっています。時として、複数のグラフを並べて描画したいときがあります。そのようなときは、描画する際の設定モード(parameter)のオプション指定を行います。複数描画の場合には、mfrow( )を使います。使用後は、デフォルトの設定に戻しておきます。

par( mfrow=c( 行数, 列数 ))　　# グラフ画面を行数×列数に分割する
　　　　　　　　　　　　　　　 # 複数のグラフを同時に描画する

4.2.2 回帰直線を追加する

散布図の上に、回帰直線を追加することができます。直線を引くにはlines( )関数を用いますが、２つの点のＸ座標とＹ座標の値を指定する必要があります。ｙ切片ａおよび傾きｂの値がわかっているときには、abline( )関数を使います。
　直線に関しても、線の種類、色や太さなどをオプション指定することができます。

lines( c(x1, x2), c(y1, y2)　　# 点A(x1,y1)と点B(x2,y2)
　　　type="l" )　　　　　　　 # 直線を指定するオプションが必要
abline(a=切片, b=傾き)　　　　　 # y=a+bxの直線を追加
オプション lty=直線の種類を数値で# １：実線、2：破線 3:点線 4:点・破線 5:長い破線
　　　　　 lwd=直線の太さ　　　　# デフォルトは１

回帰直線の値を求めるには、線形モデルlm( )を使って回帰分析を行う必要があります。回帰分析の結果の要約はsummary( )で示されます。この結果を見て、abline( )関数に切片(intecept)と傾きの推定値(estimate)を入力するか、あるいは、回帰分析の結果を引数として渡すこともできます。

lm( 変数1 ~ 変数2 )　　　　　# 変数2を要因として、変数1を回帰分析
summary(lm( 変数1 ~ 変数2 )) # 回帰分析の結果を要約
abline(lm( 変数1 ~ 変数2 ))　# 回帰直線を追加

最後に、グラフ中にテキストを追加するには、text( )を使って、追加するテキストと追加する場所を指定します。場所を座標(x,y)で指定することもできますが、locator(1)とするとマウスによって場所指定することもできます。指定座標やマウスの＋の位置が、貼り付けられるテキストの中心となります。
　テキストをグラフの周辺に追加するには、mtext( ) を使います。（ｍはmarginの意味です）４つの周辺がありますので、数値で場所を指定します。side=3とするとグラフの上辺に表示されますが、これは主タイトル（グラフキャプション）よりも下の位置です。

text( x座標, y座標, "テキスト文字列" )　　# 改行文字は&backslash;n
text( locator(1), "テキスト文字列" )　　　# マウスで場所を指定
mtext( "テキスト文字列", side=数値 )　# 1:下 2:左 3:上 4:右

[4.3] 相関行列、散布図行列

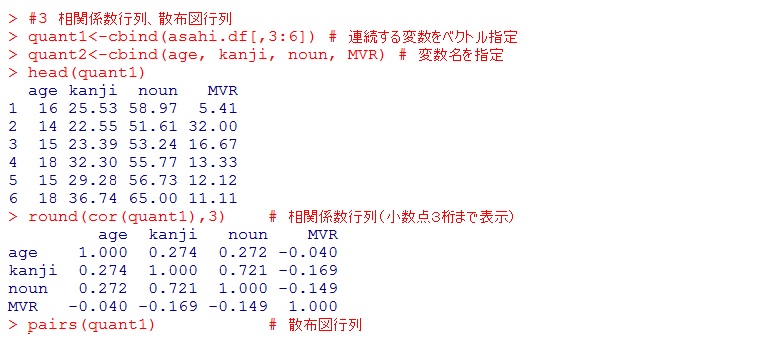
複数の変量の間の、２変量の相関係数や散布図を総当たりで求めることができます。cor( )あるいはpairs( )関数に、対象となる変数をベクトルにして渡します。
対象となる変数の列が連続しているときは ":" で指定できます。列(column)が連続していない変数を束ねるには、cbind( )関数を使って、一度新たなデータセットを作ってから、作業します。

cor( 変数のベクトル ) # 相関行列
pairs( 変数のベクトル ) # 散布図行列
cbind( 変数1, 変数2, ...) # 列変数を束ねた表データを作る

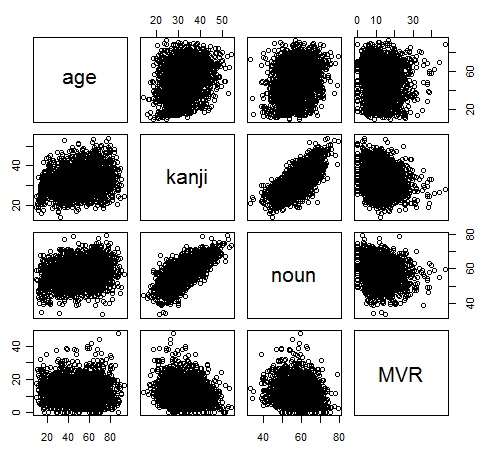
投書データの中の数量データ（年齢を含める）だけからなる新たなデータセットを作り、相関行列と散布図行列を作ってみましょう。

[4.4] 相関係数と範囲の効果

ある２変量の、全体の相関係数と、全体のうちの一部だけの相関係数を比較すると、一部だけのデータの相関係数のほうが小さくなると言われています。

全体データの中から、条件を満たす一部のデータを抽出するには、下位集合を取るsubset( )関数を用います。今、対象変数をdf, 抽出条件を指定する変数をxとします。
ここでは、「課題」に沿って、漢字率と名詞率データの一部を抽出して、全体の相関係数と比較してみます。抽出条件を年齢が30歳以上50歳未満と設定します。

subset( 対象データ, 抽出条件 )
「変数の値がある数値valに等しい」　　x == val
「変数の値がある数値val以上、以下」　x >=val, x<=val
「変数の値が文字列」　　　　　　　　 x == "要因名"

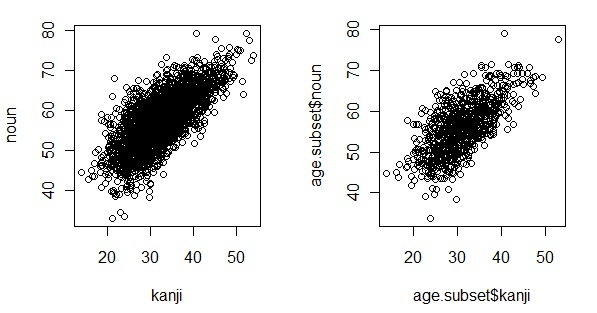
全体データの散布図と、一部データの散布図を比較するために、グラフィック画面に２つのグラフを並べて描画してみましょう。

左が全体データの散布図で、右が一部データの散布図です。散布図で相関を比較すると違いがよくわかりません。相関係数で比較すると、全体で0.72, 一部データのほうが0.68ですので、数値的には小さくなっています。