[５]　正規分布と標準化


　　[5.1] 正規分布
　　[5.2] データの標準化
　　[5.3] データの正規性

[5.1] 正規分布

5.1.1 正規分布関係の関数

Rで正規分布(normal distribution)を扱うには、dnorm( ), pnorm( ), qnorm( )などがあります。正規分布の平均meanと標準偏差sdに関して数値指定をすることができます。省略した場合は、平均0、標準偏差1の標準正規分布となります。
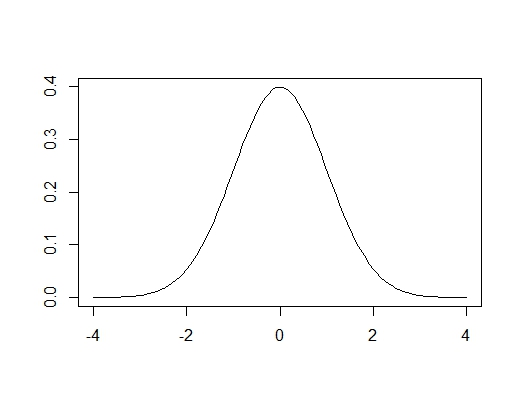
関数dnorm( )はベクトルｘに対応する正規分布確率密度を返しますので、正規分布を描画するときに使われます。dnorm( )の戻り値をplot( ) またはcurve( ) 関数に渡します。curve( ) は曲線を描くための専用関数で、dnorm(x)をそのまま渡せますので便利です。
pnorm( ) は下側確率を返しますので、上側確率は(1-下側確率）で計算できます。rnorm( )関数は、正規分布に基づくシミュレーション等で使われます。

R の関数を使いこなそう
dnorm( x, mean=m, sd=n )平均ｍ、標準偏差ｎの正規分布確率密度を返す
plot.it=F密度関数グラフを描画しない
pnorm( ｚ値 )指定したｚ値の下側確率P(z<z値)
lower.tail=F指定したｚ値の上側確率P(z>z値)
qnorm( 確率 )指定した下側確率に対応するｚ値（境界値）
lower.tail=F指定した上側確率に対応するｚ値（境界値）
rnorm( n )標準正規分布に従う乱数をｎ個生成する
plot( function(x) dnorm(x), from=始点, to=終点 )正規分布を描画
（注：from, toを省略すると-4〜4の範囲）
curve( dnorm(x), from=始点, to=終点 )from〜toの範囲の標準正規分布を描画

curve( dnorm(x), from=-4, to=4,
xlab="", ylab="" ) # 標準正規分布を描画
pnorm( 1.64 ) # P(z<1.64) 下側確率
[1] 0.9494974
pnorm( 1.94, lower.tail=FALSE ) # P(z>1.64) 上側確率
[1] 0.05050258
qnorm( 0.025) # 下側2.5%の境界値
[1] -1.959964
qnorm( 0.025, lower.tail=FALSE ) # 下側2.5%の境界値
[1] 1.959964
rnorm( 20 ) # 正規乱数を20個生成
 [1]  0.35012287  0.63656089  1.08168384  1.87580444 -0.11078253
 [6] -1.40104582 -0.85923347  1.05865120  0.92046185  2.56489108
[11]  0.41831019 -0.06304499  0.70888902 -0.93968931  0.30177921
[16] -0.91298781 -1.06880374  0.95506863 -0.86662900  0.59328784

5.1.2 グラフの特定範囲を色づけする

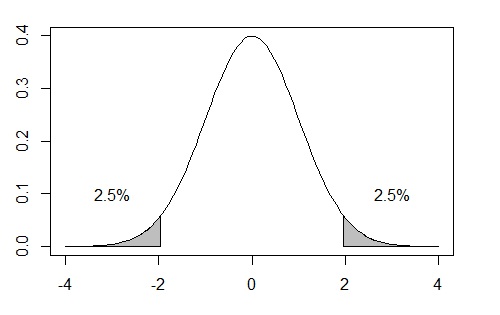
上の正規分布グラフに対し、たとえば、両側2.5％の棄却域を色づけ表示してみましょう。以下で述べるpolygon( )関数を利用する方法は、船尾暢男(2005)『The R Tips』、九天社、pp.295-6を参考にしています。

手順は、次のようになります。
(1) 正規分布(-4〜4の範囲）を描画
(2) 臨界値 -1.96 より左側を50分割し、polygon( )で塗りつぶし
(3) 右側の臨界値の右側についても同様に塗りつぶし
(4) y=0の直線を追加、（必要に応じて）テキスト文字列を追加

多角形を描くためには、まず、連続する頂点のX座標、Y座標を与える必要があります。そのような、連続する数値ベクトルを作成するためにseq( )関数、パタンを指定回数だけ繰り返すrep( ) 関数、数値ベクトルを逆順に格納する rev( ) 関数を使います。

seq( )やrep( )は、Rでデータを作成するときにとても便利で、役に立ちます。以下に、使い方の例を挙げます。戻り値を見て、コツをつかみましょう。

R の関数を使いこなそう
seq( 始点, 終点, by=区切り間隔 )指定間隔で区切られた等差ベクトル
length=区切り数指定した区切り数でベクトルを等分
rep( パタン, 繰り返し回数 )指定パタンの繰り返しベクトルを返す
（注：パタンとして、文字列、数値、ベクトルなどを指定できる
rev( ベクトル )ベクトル要素を逆順にしたベクトルを返す

rep( 0, 50 ) # 数値の繰り返し
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[31] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
rep( "文字列", 10 ) # 文字列の繰り返し
[1] "文字列" "文字列" "文字列" "文字列" "文字列" "文字列"
[7] "文字列" "文字列" "文字列" "文
rep( c(1, 2, 3), 10 ) # ベクトルの繰り返し
[1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
c( rep( "北海道", 5 ), rep( "青森県", 4 ) ) # 繰り返しパタンの結合
[1] "北海道" "北海道" "北海道" "北海道" "北海道" "青森県"
[7] "青森県" "青森県" "青森
seq( 0, 4, by=0.5 ) # 等間隔区切り（始点・終点が含まれる）
[1] 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
seq( 0, 4, length=9 ) # 範囲を９分割（始点・終点が含まれる）
[1] 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
rev( seq( 0, 4, length=9 ) ) # 逆順に並べ変える
[1] 4.0 3.5 3.0 2.5 2.0 1.5 1.0 0.5 0.0

多角形を描画するための polygon( )関数の使い方は次のようになります。

R の関数を使いこなそう
polygon( ｘ座標ベクトル、ｙ座標ベクトル )頂点の各座標(x,y)を順に直線で結んで多角形を描画し、その中を塗りつぶす
col=数値、または色名　
angle=斜線の角度左周りに0〜360度
density=斜線の密度１インチ当たりの本数

ここでの作業内容は、臨界値 -1.96 より左側の範囲を塗りつぶすことです。そのためには、X軸の直線と確率密度曲線で囲まれた部分を多くの頂点を持つ多角形と見なします。そして、各頂点を左回りまたは右回りで順に並べて、x, y座標のベクトルに形にして、polygon( )に渡します。

# 底辺直線部の座標
x <- seq( -4, -1.96, length=50 ) # x範囲を50分割
y <- rep( 0, 50 ) # y座標はすべて0
# 確率密度曲線上の座標
revx <- rev( x ) # x座標を逆向きに並べ替え
dx <- dnorm( revx ) # x座標に対応する曲線上の値（y座標）
# 直線部と曲線部の座標を合併
xvals <- c( x, revx )
yvals <- c( y, dx )
# 標準正規分布を描いて、多角形を塗りつぶして追加
curve( dnorm( x ), -4, 4, xlab="", ylab="" )
polygon( xvals, yvals, col="gray" ) # 左側2.5%棄却域の塗りつぶし
# 右側2.5%領域
xvals <- c( seq( 4, 1.96, length=50 ), seq( 1.96, 4, length=50 ) )
yvals <- c( rep( 0, 50 ), dnorm( seq( 1.96, 4, length=50 ) ) )
polygon( xvals, yvals, col="gray" )
text( -3, 0.1, "2.5%" )
text( 3, 0.1, "2.5%" )

　棄却域を塗りつぶしたグラフを描画するときに、上のようなコマンドを毎回打つのは骨が折れます。そこで、関数名をつけて、ファイルにその定義を書いておきます。たとえば、paint_region.R を用意します。そして、必要な時にsource( スクリプトファイルのパス )関数で呼び出して使うのが便利です。

　関数paint_region( )には、始点と終点のx座標の値を渡します。始点と終点はどちらを先にしてもかまいません。ただし、始点と終点のｘ座標は、標準正規分布のｘ軸の範囲内に収まるように指定してください。（この辺の処理は本来もっと厳密に、丁寧に描くべきですが、今のバージョンは簡略に書いています。）
　オプションとして、多角形の座標の数（の半分）や、塗りつぶしに使う色を文字で指定することができます。
　paint_region( )関数を使うと、上と同じグラフをずっと簡単に描くことができます。

source( "paint_region.R" )
curve( dnorm(x), -4, 4, xlab="", ylab="" ) # -4〜4の範囲で、確率分布曲線を描く
paint_region( -4, -1.96 ) # 左側棄却域塗りつぶし
paint_region( 1.96, 4 ) # 右側棄却域塗りつぶし

[5.2] データの標準化

ここでは、漢字率データを対象に、各データの偏差(deviation)、ｚ得点、および偏差値を計算し、一覧表の形で出力してみましょう。

kanji.mean <- mean( kanji )
kanji.sd <- sd( kanji )
dev <- round( kanji - kanji.mean, 3 )
zscore <- round( dev / kanji.sd, 3 )
Zscore <- round( zscore * 10 + 50, 2 )
result <- cbind( kanji, dev, zscore, Zscore )
head( result )
     kanji    dev zscore Zscore
[1,] 25.53 -6.692 -1.087  39.13
[2,] 22.55 -9.672 -1.572  34.28
[3,] 23.39 -8.832 -1.435  35.65
[4,] 32.30  0.078  0.013  50.13
[5,] 29.28 -2.942 -0.478  45.22
[6,] 36.74  4.518  0.734  57.34
mean( zscore ) # z得点の平均
[1] 7.564725e-05
sd( zscore ) # z得点の標準偏差
[1] 0.9999952
mean( Zscore ) # 偏差値の平均
[1] 50.00076
sd( Zscore ) # 偏差値の標準偏差
[1] 9.999952

理論的には、ｚ得点の平均は0、標準偏差は1です。しかし、実際の計算結果は、丸めの影響を受けて、理論値通りにはならないことがあります。上の結果中、ｚ得点の平均値が指数(exponent)表記によって7.564725e-05と表示されています。この値は、7.564725＊1/10^5 = 0.00007564725 を表します。

[5.3] データの正規性チェック

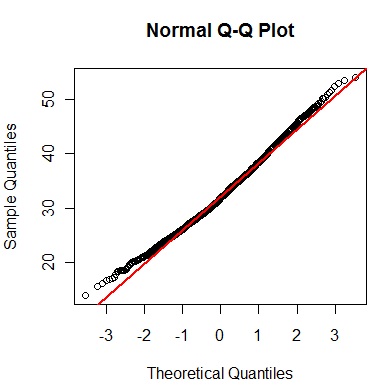
データが正規分布に従っているかどうかをチェックするには、qqnorm( )関数を用います。この関数に、データ変数名を与えると、対象データの順序標本（昇順に並べたデータ）と、正規分布から選ばれた同数の順序分位点に対してプロットした散布図を作ります。

R の関数を使いこなそう
qqnorm( データ名 )Q−Qプロットを描画する
qqline( データ名 ）完全な正規分布に従うときの予想線
lwd=n線の太さ（デフォルトは1）
col="色名"1:黒 2:赤 3:青 4:緑 5:水色 6:茶

qqnorm( kanji )
qqline( kanji, lwd=2, col="red" )

対象データが正規分布に完全に従うときには、データの点列が、図中の赤線の上に直線状に並びます。漢字率データは、ほとんどが赤線の近くに並んでいるので、ほぼ正規分布をしていると見なせます。