
| [6.1] ランダム抽出 |
| [6.2] シミュレーション |
(有限)母集団から指定された個数のデータをランダムに抽出するには、sample( )関数を用います。一方、(標準)正規分布から指定された個数のデータをランダム抽出する場合は、rnorm( )関数を使います。
| R の関数を使いこなそう | |
| sample( 母集団ベクトル, 抽出データ数 ) | 母集団から指定個データをランダム抽出する |
| replace=T | 一度抽出されたデータを復元してからデータ抽出する (省略時は非復元抽出) |
| rnorm( 抽出データ数 ) | 正規分布から指定された個数のデータを抽出する |
| mean = 値 | 正規分布の平均値を指定、省略時は0 |
| sd = 値 | 正規分布の標準偏差を指定、省略時は1 |
朝日新聞投書データセット(asahi.df)の中に文長(slength)データがあります。この文長データを有限母集団とし、10個のデータをランダムに抽出してみます。
大数の法則(the law of large number)とは、ある試行を何回も行えば、確率は一定値に近づくという法則です。たとえば、ある母集団から標本を抽出を繰り返し行い、抽出された標本の平均値の平均を求めると、母平均に近づいていきます。
朝日新聞投書データセット中の文長(slength)データを有限母集団として使って、大数の法則が当てはまるか、シミュレーションで確認してみましょう。
この母集団はμ=38.56(文字)、σ=9.38です。今、この母集団から標本サイズN=5の標本を、1個から1000個まで取り出します。そして、抽出標本の平均値の平均を計算して、ベクトル変数Smeanに格納します。変数Smeanの値が、母平均38.56に近づいていくかどうかを観察しましょう。
| R の関数を使いこなそう | |
| mtext( message ) | 文字列変数messageをグラフ枠の外marginに出力 |
| side=値 | 出力位置(1:下、2:左 3:上 4:右)、省略時は上 |
| cex=値 | 文字拡大比率(char expansion)、省略時は1.0 |
| font="フォント名" | 使用フォントを指定 |
| paste( a, "string", c ) | 文字列変数や文字列定数を順番につなぎ合わせる |

|
上の図では平均値が理論値に近づいていく様子を確認できますが、必ずしもそうはならないこともあります。ここでは1000回の標本抽出を行いましたが、回数を増やすと理論値に近づいていき、大数の法則が成り立つことが確認できます。
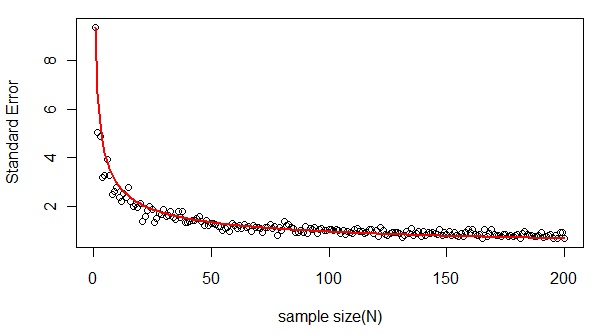
標本抽出分布の標準偏差を標準誤差(standard error, SE)といい、統計分析において重要な役割を果たします。標準誤差の大きさは標本サイズNが大きくなるほど小さくなり、SE=σ/sqrt(N)という理論値に近づくとされます。ここでは、抽出回数を20回で固定しておき、標本サイズだけを1〜200まで大きくしていきます。そのとき、20個の平均値データの標準偏差(標準誤差)がどのように推移するか、シミュレーションしてみましょう。
|
赤い曲線は理論値です。シミュレーションの結果、ほぼ理論の予測通り、標準誤差の大きさは標本サイズが大きくなるにつれて急速に小さくなる様子が観察されます。
最後のシミュレーションは、中心極限定理(the central limit theorem)です。この定理は、たとえ母集団が正規分布でなくても、標本サイズが大きくなると、標本平均値の分布は正規分布に近づいていく、というものです。理論的には、その正規分布の平均は母平均μ、標準偏差はσ/√Nとなります。
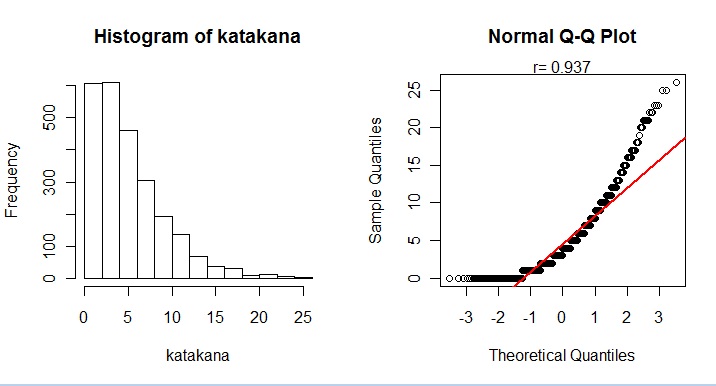
ここでは、母集団としてカタカナ語使用回数データを使うことにします。このデータは離散変数で、ヒストグラムや Q-Qプロットが示すように、明らかに、正規分布ではありません。
|
このカタカナ使用回数の母集団の平均は4.583、標準偏差は4.073です。この母集団から、標本サイズを1〜100まで徐々に大きくしながら、毎回100個ずつ標本抽出を行います。100個の標本平均データに対して、正規性の尺度として相関係数を計算し、ベクトル変数に格納していきます。中心極限定理は、標本サイズが大きくなるにつれて標本抽出分布が正規分布に近づくと予測しますので、計算した相関係数が1に近づくと予測します。
| R の関数を使いこなそう | |
| 変数 <- qqnorm( ベクトル変数 ) | QQプロットを描く、戻り値を格納 |
| plot.it=F | QQプロットを描画しない |
| cor( ret$x, ret$y ) | 理論値xと元データyの相関を求める |
| mtext( message ) | 文字列変数messageをグラフ枠の外marginに出力 |
| side=1,2,3,4 | 出力位置(1:下、2:左 3:上 4:右)、省略時は上 |
| cex=値 | 文字拡大比率(char expansion)、省略時トは1.0 |
| font="フォント名" | 使用フォントを指定 |
| paste( a, "string", c ) | 文字列変数や文字列定数を順番につなぎ合わせる |

[6.3] シミュレーションの関数化一連の計算処理をひとまとめにして、関数化すると便利です。計算に必要な変数は、引数で指定します。ここでは、6.2節で行った3つのシミュレーションを行う関数を作成します。 6.3.1 large.number( )最初は、標本サイズと標本抽出分布の平均の推移です。必要な引数は、母集団データpop、標本サイズsize、抽出回数timesの3つです。
l
arge.number <- function( pop, size, times ) {
Smean<-vector(length=times) sum <- 0 for ( i in 1:times ) { xbar <- mean( sample( pop, size ) ) sum <- sum + xbar Smean[i] <- sum / i } plot( Smean, main="標本抽出回数と抽出分布平均", xlab="抽出回数", ylab="標本抽出分布の平均" ) myu <- mean( pop ) pop.str <- deparse( substitute( pop ) ) mtext( paste( "population=", pop.str, ", μ=", round(myu, 3), ", sample size=", size ) ) abline( h=myu, col="red", lwd=2, lty=2 ) } large.number( noun, 10, 500 ) 6.3.2 stderr( )
stderr <- function( pop, size, times ) {
y <- vector(length=size) data <- vector(length=times) for ( i in 1:size ) { for( j in 1:times ) { data[j] <- mean( sample( pop, i ) ) } y[i] <- sd( data ) } x <- 1:size plot( x, y, xlab="sample size(N)", ylab="Standard Error", axes=F ) y <- sd(slength)/sqrt(x) # 理論値を代入 par( new=T ) # 理論値曲線を追加 plot( x, y, type="l", col="red", ylab="", xlab="", lwd=2 ) } stderr( slength, 200, 50 ) 6.3.3 central.limit( )
central.limit <- function( pop, size, times ) {
r <- vector( length=size ) # 相関係数データを格納するベクトル for ( i in 1:size ) { mean.data <- vector( length=times ) for ( j in 1:times ) { mean.data[j] <- mean( sample( pop, i ) ) } ret <- qqnorm( mean.data, plot.it=F ) # QQプロットを描画せず r[i] <- cor( ret$x, ret$y ) # 相関係数を格納 } plot( 1:size, r, ylim=c(0.90, 1 ), xlab="標本サイズ", ylab="正規分布との相関係数", main="中心極限定理のシミュレーション" ) } central.limit( katakana, 100, 50 )
|