[7] 統計的検定と推定の方法
[7.1] 1つの平均値の検定と推定
すでに学習した通り、検定の手順は、
- 帰無仮説と対立仮説を立てる(片側検定か両側検定かが決まる)
- 有意水準αに基づいて、利用する確率分布における境界値を求める
- 検定量を計算する
- 検定量と境界値を比較して、結論を出す。検定量以上の値が得られる確率を求める。
上のステップ2において境界値を計算するときには、qnorm( ), qt( ) という、qのついた関数を使います。ステップ4において、得られた検定量に対応する有意確率を計算するときには、pnorm( ), pt( )のように、pのついた関数を使います。
| R の関数を使いこなそう |
| qnorm( p ) | 標準正規分布上で、確率pに対応するzの値(境界値)
両側検定のときはp/2とする。2つの境界値は±戻り値 |
| qt( p, df ) | 自由度dfのt分布上で、確率pに対応するtの値
両側検定のときはp/2とする。2つの境界値は±戻り値 |
| pnorm( z0 ) | 標準正規分布における検定量z0に対する下側確率P(z<z0)
両側検定のときは、この値を2倍する |
| lower.tail=FALSE | FALSEを指定すると上側確率P(z>z0) |
| pt( t0, df ) | 自由度dfのt分布における検定量t0に対する下側確率P(t<t0)
両側検定のときは、この値を2倍する |
| lower.tail=FALSE | FALSEを指定すると上側確率P(t>t0) |
7.1.1 平均値の検定と推定
(例題)ある年の某新聞投書データ2472件について、投書者の年齢を調査したところ、平均は51.12歳、標準偏差は17.19である。この結果から母集団投書者の平均年齢は50歳以上であるとみなしてよいか。有意水準5%で検定しなさい。
また、この標本データに基づいて母集団の平均年齢を95%信頼度で推定しなさい。
( N <- length(age) )
[1] 2472
( t <- abs(qt(0.05/2, N-1)) ) # 境界値(両側検定なので、α/2)
[1] 1.960924
mu <- 50
(t0 <- ( mean(age) - mu) / (sd(age) / sqrt(N))) # 検定量
[1] 3.246009
2 * pt( t0, N-1, lower.tail=FALSE ) # 上側確率
[1] 0.001185989
# 95%信頼区間の推定
SE <- sd(age) / sqrt(N)
(lower <- mean(age) - t * SE)
[1] 50.44426
(upper <- mean(age) + t * SE)
[1] 51.80007
N=2472の大標本ではありますが、母分散が未知なので、t分布を用いて検定を行います。検定量t0=3.246が境界値1.96よりも大きいので、帰無仮説H0: μ=50 を棄却します。また、95%信頼区間を計算すると、(50.44〜51.80)となり、間に50を含まないことが確認できます。
1標本の平均値から母平均の検定を行うには、Rの組み込み関数 t.test( ) に、データ名、母平均、および検定のモードを指定することで、同じ結果を得ることができます。
t.test(age, mu=50, alternative="two.sided")
One Sample t-test
data: age
t = 3.246, df = 2471, p-value = 0.001186
alternative hypothesis: true mean is not equal to 50
95 percent confidence interval:
50.44426 51.80007
sample estimates:
mean of x
51.12217
| R の関数を使いこなそう |
| t.test( データ名, mu=x ) | 1つの平均値に対する検定 |
| alternative="greater" | 右片側検定 |
| alternative="less" | 左片側検定 |
| alternative="two.sided" | 両側検定 |
7.1.2 平均値と信頼区間を図示
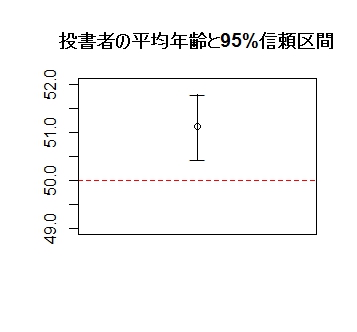
年齢の平均値とその95%信頼区間、および比較値を描画してみると、視覚的にも検定、推定の結果を理解しやすくなります。
下限値と上限値を"-"記号で示し、それらを直線で結びます。2点を結ぶ直線を引くには、lines( )関数を使います。グラフ中に直線を追加するには、abline( )関数を用います。
| R の関数を使いこなそう |
| plot( x, y ) | データ(x, y)をプロットする |
| axes=FALSE | X軸、Y軸など軸を表示しない
必要な軸はaxis( )を使って指定する |
| axis( side=1/2/3/4 ) | 1:下(X軸)
2:左(Y軸)
3:上(第2X軸)
4:右(第2Y軸) |
| points( x, y ) | データ(x, y)をグラフに追加する |
| lines( c(x1, x2), c(y1, y2) ) | 座標(x1, y1), (x2, y2)を結ぶ直線を追加する |
| abline( a=a, b=b ) | y切片a, 傾きbの直線を追加する |
| abline( h=h ) | y=hの水平線を追加する |
| abline( v=v ) | x=vの垂直線を追加する |
| box() | 図を枠線で囲む |
plot( 1, mean(age), ylim=c( 49, 52 ), xlim=c( 0, 2 ),
axes=F, xlab="", ylab="" )
axis( 2 )
points( 1, upper, pch="―" ) # 上限値
points( 1, lower, pch="―" ) # 下限値
lines( c(1, 1 ), c(lower, upper), lwd=1 )
abline( h=50, lty=2, col="red" ) # 比較値
title( "投書者の平均年齢と95%信頼区間" )
box()
[7.2] 1つの割合の検定と推定
すでに学習したように、標本サイズが30以上の場合は、検定量が標準正規分布に近似することを利用できます。
7.2.1
(例題)ある年の某新聞投書データのうち、女性の投書の中で擬音語が使われているかどうかを調べたところ、次のような結果が得られた。
| 使用なし | 使用あり | 合計 |
| 494 | 712 | 1206 |
| 41.0% | 59.0% | 100.0% |
母集団において女性の擬音語使用率を60%とみなしてよいだろうか?有意水準5%で検定しなさい。
また、この標本データに基づいて母集団の平均擬音語使用率の95%信頼区間を推定しなさい。
# 1つの母比率の検定
( p0 <- 712/1206 ) # 標本比率
[1] 0.5903814
( z <- qnorm( 0.05/2, lower.tail=F ) ) # 境界値(両側)
[1] 1.959964
pi <- 0.6 # 比較値
N <- 1206 # 標本サイズ
T <- ( p0 - pi ) / sqrt( pi * ( 1 - pi ) / N ) # 検定量
[1] -0.6818341
pnorm( T ) * 2 # 有意確率(両側なので2倍)
[1] 0.4953439
# 母比率の区間推定
( p0 - z * sqrt( p0 * ( 1-p0 ) / N ) ) # 下限値
[1] 0.5626271
( p0 + z * sqrt( p0 * ( 1-p0 ) / N ) ) # 上限値
[1] 0.6181357 # 推定区間は0.6を含んでいる