[8] 分散分析と多重比較
[9.1] 一元配置分散分析
9.1.1 3つ以上の母分散の等質性の検定
3つ以上の標本の母平均が等しいかどうかを検定するには分散分析を用います。分散分析を行うためには、分布の正規性と等分散性が前提とされています。
等分散性の検定には、ハートレー法、F検定、バートレット検定などがあります。ハートレー(Hartley)の方法は、最大分散と最小分散の比FmaxをStudentの範囲の表の境界値と比較しますが、母分散が正規でないときには望ましくないとされています。ここでは、バートレット(Bartlett)の検定を行うこととします。
Rでバートレット検定を行うには、bartlett( )関数の引数として、対象データをフォーミュラ形式(数量データ~カテゴリデータ)で渡します。
【例題】新聞投書データを投稿者の年齢に応じて、若年(25歳未満)、壮年(45歳未満)、熟年(65歳未満)、老年(65歳以上)という4つのグループに分割する。文長データに関して、各年齢層の母分散が等しいをいえるかどうかどうかを有意水準5%で検定しなさい。
この課題をRで解くために、まず、年齢のカテゴリデータage.classを作成し、その後、bartlett.test( )に、文長データ~年齢カテゴリデータというフォーミュラを渡します。年齢データを条件ごとに年齢層に分割するには、ifelse( )関数を使います。つくられるカテゴリを"young", "adult", "mature", "old" と名づけると、Rのデフォルトに従ってアルファベット順に並べられます。「若年」〜「老年」の順に並べる(出力させる)ためには、levels=c( "young", "adult", "mature", "old" ) と指定します。
# 年齢カテゴリを作成する
age.class
age.class <- ifelse( age < 25, "young", ifelse( age < 45, "adult",
ifelse( age < 65, "mature", "old" ) ) )
age.class <- factor( age.class, levels=c( "young", "adult", "mature", "old" ) ) # カテゴリの要因の順序づけ
head( cbind( age, age.class ) )
age age.class
[1,] "16" "young"
[2,] "14" "young"
[3,] "15" "young"
[4,] "18" "young"
[5,] "15" "young"
[6,] "18" "young"
# 等分散性の検定をする
bartlett.test( slength ~ age.class )
Bartlett test of homogeneity of variances
data: slength by age.class
Bartlett's K-squared = 14.3023, df = 3, p-value = 0.002521
Bartlett検定の検定量は、自由度df=(カテゴリ数-1)のχ2分布に従います。検定の結果、5%レベルで有意ですので、4つの年齢データの母分散が等しくないと結論されます。
(注)Rの一元配置分散分析では、デフォルトで、母分散が等しくないと仮定して、対応しています。
| R の関数を使いこなそう |
| bartlett.test( 数量データ~カテゴリデータ ) | カテゴリごとの対象データ |
| ifelse( 条件, 値1, 値2 ) | 条件が満たされるときは値1、満たされないときは値2を返す
条件分岐の結果を保存するには変数に代入する |
9.1.2 一元配置分散分析
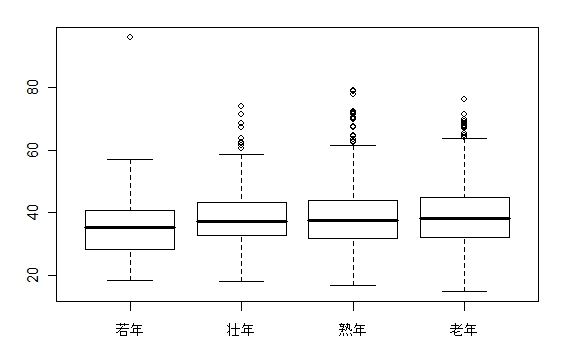
検定を行う前に、文長データを年齢層ごとに層分けして箱ひげ図を描画すると、データを視覚的に把握するのに役立ちます。層別の箱ひげ図を描画するには、boxplot( ) 関数にフォーミュラを渡します。
# 年齢層別の文長データ箱ひげ図
age.class.names <- c( "若年", "壮年", "熟年", "老年" )
boxplot( slength ~ age.class, names=age.class.names, main="年齢層別の文長データの箱ひげ図" )
一元配置分散分析oneway.test( )の場合も、bartlett.test( ) や boxplot( ) と同じフォーミュラを引数として渡すことができます。
oneway.test( slength ~ age.class )
One-way analysis of means (not assuming equal variances)
data: slength and age.class
F = 9.3732, num df = 3.000, denom df = 813.137, p-value = 4.278e-06
結果で表示されているように、分散が等しくないと仮定して、検定が行われています。(等分散のときは、オプションでvar.equal=TRUE と指定します) 返されたP値から、有意水準5%レベルで帰無仮説「母平均は等しい」が棄却されます。したがって、4つの年齢層の母平均のどこかに有意な差があるという結論が得られます。
[9.2] 多重比較
分散分析の結果有意となったことを受けて、事後比較として、どの年齢層間に平均値の有意差があるのかを調べる作業に進みます。
その前に、各年齢層の文長平均値を求めて、全部の年齢層間の平均値差を計算しておきましょう。Rではtapply( ) 関数を使うと、層別された統計量等の値を簡単に求めることができます。
ただし、後の分析のためにsubset( ) 関数を使って、年齢層ごとのデータを作成しておきましょう。
# 各年齢層の文長平均値を求める
tapply(slength, age.class, mean)
young adult mature old
35.52404 38.51754 38.68103 39.38357
# 各年齢層データを作成する
head( slength.young <- subset( slength, age.class=="young" ) ) # 若年層文長データ
[1] 26.25 27.92 35.14 38.30 45.13 52.89
head(slength.adult <- subset( slength, age.class=="adult" ) ) # 壮年層文長データ
[1] 24.75 22.23 21.93 26.92 36.69 36.08
head(slength.mature <l;- subset( slength, age.class=="mature" ) ) # 熟年層文長データ
[1] 53.80 46.27 28.93 28.45 38.92 31.08
head(slength.old <- subset( slength, age.class=="old" ) ) # 老年層文長データ
[1] 41.55 45.00 51.89 33.86 65.40 39.80
# 年齢層間の平均値差
mean( slength.adult ) - mean( slength.young )
[1] [1] 2.993505
mean( slength.mature ) - mean( slength.young )
[1] [1] 3.156989
mean( slength.old ) - mean( slength.young )
[1] 3.85953
mean( slength.mature ) - mean( slength.adult )
[1] 0.1634842
mean( slength.old ) - mean( slength.adult )
[1] 0.866025
mean( slength.old ) - mean( slength.mature )
[1] 0.7025409
9.2.1 ボンフェローニ法
ボンフェローニ(Bonferoni)法では、t検定を用いて2群間の平均値差の検定を行いますが、その際、ある有意水準を多重比較を行う回数(t検定を行う回数)で割った値をt検定の有意水準とします。今の場合では、4年齢層を総当りで比較すると6回t検定を行うことになるので、全体の有意水準を0.05とすると、各回のt検定の有意水準は、0.05/6=0.0083となります。
例として、若年と壮年間で平均値差があるか、t検定します。var.test( )によって等分散性の検定を行ったのち、t.test( )に若年と壮年のデータを渡します。
var.test(slength.young, slength.adult)
Two Sample t-test
data: slength.young and slength.adult
t = -4.3196, df = 881, p-value = 1.741e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.353637 -1.633373
sample estimates:
mean of x mean of y
35.52404 38.51754
t.test(slength.young, slength.adult, var.equal=T)
F test to compare two variances
data: slength.young and slength.adult
F = 1.0776, num df = 202, denom df = 679, p-value = 0.4941
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.8683828 1.3554846
sample estimates:
ratio of variances
1.077588
9.2.2 テューキー法
テューキー法(Tukey's method)では、2群の平均値差を、有意水準に対応する境界値HSDと比較して判定します。Rでは、aov( )関数によって分散分析を行い、その結果と、カテゴリ変数の名前をtukeyHSD( )関数に渡します。
# (一元配置)分散分析の結果
summary( res <- aov( slength ~ age.class, data=asahi.df ) )
Df Sum Sq Mean Sq F value Pr(>F)
age.class 3 2318 773 8.8661 7.635e-06 ***
Residuals 2468 215047 87
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0
# Tukey 法で多重比較
TukeyHSD(fm2, "age.class", ordered=T)
Tukey multiple comparisons of means
95% family-wise confidence level
factor levels have been ordered
Fit: aov(formula = slength ~ age.class, data = asahi.df)
$age.class
diff lwr upr p adj
adult-young 2.9935047 1.0742312 4.912778 0.0003643
mature-young 3.1569889 1.3019910 5.011987 0.0000745
old-young 3.8595298 1.9250536 5.794006 0.0000019
mature-adult 0.1634842 -1.0411388 1.368107 0.9854200
old-adult 0.8660251 -0.4577187 2.189769 0.3334726
old-mature 0.7025409 -0.5261593 1.931241 0.4559487
[1]
[1]
| R の関数を使いこなそう |
| tapply( 対象データ, 層カテゴリデータ, 統計量 ) | カテゴリごとの対象データの統計量を計算する |
| bartlett.test( 対象変数 ~ カテゴリ変数 ) | k群間の等分散性の検定。カテゴリ変数の水準間で分散が等しいかどうかを検定する |
| oneway.test( 対象変数 ~ カテゴリ変数 ) | 一元配置分散分析。カテゴリの水準間で母平均が等しいかどうかを検定する。
(分散が等しくないと仮定している) |
| aov( 対象変数 ~ カテゴリ変数 ) | 分散分析。カテゴリの水準間で母平均が等しいかどうかを検定する。
分散分析表を表示するには、summary( ) に渡す。 |
| TukeyHSDaov( aov( 対象変数 ~ カテゴリ変数 ) ) | テューキー法による多重比較。カテゴリの水準間で母平均の差が有意かどうかを判定する。 |

