・中心傾向:周辺の異常値の、平均値、中央値に対する影響
・散布度:平均値から離れたデータの頻度(柱の高さの分布)
・分布の形:平均値を境に左右対称か?(歪み)、柱の高さ(尖り)
平均値±標準偏差の範囲にあるデータの割合(正規性)
| [3.1] 中心傾向の代表値 |
| [3.2] 散布度の代表値 |
| [3.3] 基本統計量 |
| [3.4] カテゴリデータの散ら ばり指数の算出 |
サンプルの度数分布の様子を表す、いくつかの数値。
・分布の中心傾向を表す代表値
・散らばり具合を表す代表値
(計量)データの総和をデータ数で割った値。 X = ∑Xi / N
異常値の影響受けやすい。
データを大小順に並べたとき中央に位置するデータの値。
データ数が偶数なら、中央の2つのデータの平均値を求める。
(カテゴリデータ)もっとも頻繁に生じる(度数のもっとも多い)データ。
左右対称の分布:Mean = Median = Mode
正に歪曲した分布:Mode < Median < Mean
負に歪曲した分布:Mean < Median < Mode
範囲:観測データ中、最小の値と最大の値の差。
全データの重心(平均値)と各データとの差に基づいて計算される散らばり具合を表す数値。
一般にデータが平均値付近に集まっているときには小さな値、広い範囲に散らばっているときは大きな値となる。
偏差:(各データの値 -
平均値)の値。偏差を総和すると0になる。
↓
偏差平方和:各データの偏差を2乗する。(必ず正の値)。その総
和を求める。
↓
分散(Variance):偏差平方和をデータ数で割った値。V
= ∑(Xi - X)2 / N - 1
標本分散(V):データ数 N - 1 で割る =var( data )
母集団の分散(σ2):データ数 N で割る =varp( data )
↓
標準偏差(Standard
Deviation):分散の平方根の値。 S = √V
↓
変動係数:(標準偏差 / 平均値 * 100 )の値。
異なるデータ同士でも散らばり具合を比較できる。
分布のひずみ具合(左右非対称の度合い)を表す尺度。
左右対称なら0の値、左寄りなら正の値、右寄りなら負の値となる。
データが平均値の近くにどの程度集まっているかを示す尺度。
3以上の大きな値:データが平均値付近に密集
0に近い小さな値:データが幅広く分布
「年齢ヒストグラム」シートにおいて、中心傾向の代表値を算出してみよう。
・平均値 =average( data )
・中央値 =median( data )
・モード =mode( data )
「年齢ヒストグラム」シートにおいて、散布度の代表値を算出してみよう。
■ 新しい列を挿入する
新しい列を挿入したい列(B 列)を選択した状態で、「挿入」メニューから「列」を選択。
新しい列が挿入され、従来のB列がC列に移動する。
■ 偏差を計算する:(データ Xi - 平均値 )
B1に「偏差」と入力する。
B2に A2 のデータの偏差を計算する。( =データセル - 平均値セル)
B2の計算式をB2473まで複写して、各データの偏差を計算する。
■ 偏差の総和を計算する
B2474に=sum(B2:B2473)と入力して偏差の総和を計算する。
偏差の総和は0になる。(散布度の尺度として使えない!)
■ 偏差平方和を計算する
C列に、新しい列を挿入し、列ラベル「偏差平方」を入力する。
C2に、C1 の平方を算出する。
C2の計算式をC2473まで複写して、各偏差平方を算出する。
C2474に「偏差平方和」と入力し、C2475に偏差平方和を計算する。
■(標本)分散を計算する:偏差平方和/(データ数-1)
C2476に「標本分散」と入力し、C2477に標本分散を計算する。
標本分散 =var( data )
■(標本)標準偏差を計算する:標本分散の平方根 =sqrt(標本分散)
C2478に、標本標準偏差を計算する。
標本標準偏差 =stdev( data )
■ 変動係数を計算する
変動係数 =(標準偏差/平均値)*100
C2479に「変動係数」と入力し、C2480に変動係数を計算する。
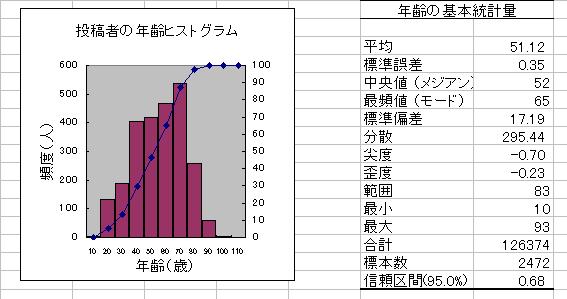
年齢データの基本統計量を算出してみよう。
「分析ツール」から「基本統計量」を選択する。
「基本統計量」ダイアログにおいて、
「入力範囲」を指定する。→キー入力またはマウスでドラッグ選択
「出力オプション」欄の、「統計情報」にチェックを入れる。
「平均の信頼区間の出力」にチェックを入れ、デフォルトの「95」%を使う。
「出力先」として、適当なセル番地(ヒストグラムの隣のセル)を指定する。
「OK」ボタンを押すと、一連の基本統計量の計算結果が表示される。
ヒストグラムと基本統計量によるデータの読み取り

・中心傾向:周辺の異常値の、平均値、中央値に対する影響
・散布度:平均値から離れたデータの頻度(柱の高さの分布)
・分布の形:平均値を境に左右対称か?(歪み)、柱の高さ(尖り)
平均値±標準偏差の範囲にあるデータの割合(正規性)
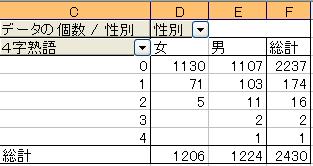
(男女別の)四字熟語データから、男女別の散らばり指数を計算してみよう。
散らばり指数:識別可能な対の最大値に対する実際の識別可能な対の数
の割合。識別可能な対の数は、
両カテゴリーに等しく配分されているときに最大、1つのカテゴリに集中しているときに
最小(0)になる。
D = c( N2 -
Σnj2 )
/ N2(
c - 1 )
( c:カテゴリ数、N:観測値の総数、n:カテゴリ内の観測値の数 )
D は、0~1の間の値を取る。1に近いほど、散らばりが大きい。