| [4.1] 相関と相関係数 |
| [4.2] 相関と散布図 |
相関:一対の変数 X と Y の間の直線的な関係。X が大になれば Y も大になるか、逆に、X が大になれば Y が小になるという関係。
相関があるからといって、ただちに、それらの間に因果関係が成り立つことを意味するわけではない。
(例:成人男性の身長と体重の関係、英語の成績と数学の成績の関係)
回帰:2つの変数間の線型的相関関係に基づいて、一方の変数の値から 他方の変数の値が予測できる。その関係を記述する直線を回帰直線という。
相関係数:2つの変数 X, Y の相関の直線的な強さを表す指標。
ピアスンの積率相関係数 r = XとYの共分散 / Xの標準偏差 * Yの標準偏差
(標本の相関係数は r, 母集団の相関係数はρで表す。)
共分散:Xの偏差とYの偏差の積を総和し、データ数 (N - 1) で割った値。
共分散 Sxy =Σ (Xi - X)(Yi - Y) / ( N - 1 )
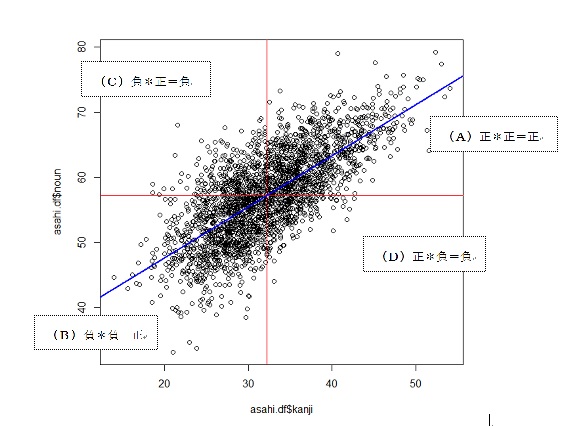
A… Xの偏差、Yの偏差が2つとも正ならば、その積は正となる。
B… Xの偏差、Yの偏差が2つとも負ならば、その積は正となる。
C… Xの偏差が正、Yの偏差が負ならば、その積は負となる。
D… Xの偏差が負、Yの偏差が正ならば、その積は負となる。
A, B のデータが多いと、2つの偏差の積の総和(共分散)は正となる。→正の相関
C, D のデータが多いと、2つの偏差の積の総和(共分散)は負となる。→負の相関
A, B, C, D に平均して分布していると、共分散は0に近づく。→相関なし。
rは、 -1 <= r <= 1 の値をとりうる。r=|1| のとき、完全な線型関数。
r > 0 のとき、正の相関、 r < 0 のとき負の相関。
| |r| の値 | rの(一般的な)解釈 |
|---|---|
| 1 | 2変量間に完全な線型相関がある |
| 0.9 以上 | 2変量間に非常に高い相関がある |
| 0.7 以上 0.9 未満 | 2変量間に高い相関がある |
| 0.3 以上 0.7 未満 | 2変量間に中くらいの相関がある |
| 0.3 未満 | 2変量間に低い相関がある |
| 0 | 2変量間に全く線型相関がない |
相関と因果関係 … 相関関係は因果関係を必ずしも含意しない。
見かけの相関 … 第3の変数Zの存在によって、XとYの表面上の相 関が高くなることもあり得る。
決定係数 r2 … Xの分散によって説明さ れるYの分散の比率=相関係数の2乗。比例尺度として比較が可能。
説明できない比率=非決定係数 k2 = 1 - r2
・範囲の効果 … 全体の母集団からの標本ではなく、一部分だけの標本に基づいて算出すると偏った相関が得られる。(切断の効果)
一般に、一部分の下位標本についての相関は、全範囲の標本の相関よりも低くなる。
・群合併の効果 … 平均値において異なる2つの群を合併して計算すると誤って高い相関が得られる。
・2次的関係 … 半円形に分布するX, Y は2次的関係があるが、直線的相関係数は0に近い。
ファイ係数:変数の取りうる値が2種類だけ(たとえば性別、病歴・喫煙の有無など)変数(2値変数)のデータから2×2分割表(クロス集計表)を作り、計算される特殊な相関係数。
φ = sqrt( χ2 / N )
ここで、χ2 = ∑{(Oj-Ej)2 / Ej}このファイ係数は、0から1までの間の値を取り、2つの2値変数の連関の強さを表します。(第10回参照)
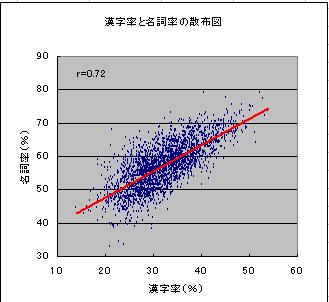
新聞投書データにおける名詞率と漢字率の相関を調べよう。
■ 数量データの準備
新しいブックを開き、Sheet1に「漢字率・名詞率相関」とタイトルを入力する。
データ表シートの漢字率データを新しいワークシートA列に、名詞率データをB列にコピーアンドペーストする。
■ 相関係数を計算する
F列に「漢字率の平均」、「名詞率の平均」と入力、G列にそれぞれの値を計算する。
C列に「漢字率の偏差」、D列に「名詞率の偏差」を計算し、C列とD列の散布図を図示する。
E列に「偏差の積」と入力し、(漢字率の偏差*名詞率の偏差)を計算する。
E列下に「共分散」と入力し、E列の総和/(データ数-1)を計算する。
E列下に「相関係数」と入力し、共分散/(漢字率の標準偏差*名詞率の標準偏差)を計算する。
相関係数: =correl( data1, data2 )
■ 散布図を描く
グラフウィザードから、「散布図」を選択。
データ範囲を指定(「先頭をラベルとして使用」にチェック)。
「目盛」タブで、最大値、最小値を調節。(グラフ領域全体にわたって表示するように。)
タイトル、X軸ラベル、Y軸ラベルを入力(凡例は不要)。
「データ系列の書式設定」で、データ表示のスタイル、サイズを調整。
■ 回帰直線と相関係数を追加
グラフ中の任意の点を右クリックし、「近似曲線の追加」を選択するとダイアログが開く。
ダイアログパネルで、「線形近似」を選択し、「回帰式」と「R-2乗値」の表示にチェックを入れる。
表示されたテキストの位置を適切な場所に配置する。
(注)マウスをドラッグしてテキストボックスを作り、テキストをキー入力して、適当な場所に移動してもよい。

■ 回帰直線 … 2つの変数間の関係を記述する直線。
回帰直線 Yyx = ayx + byxX
(Y:Xにより予測されるYの値、a, b :回帰定数)
最小2乗法 … 実際のYと予測されるYとの誤差(予測誤差)の2乗和をもっとも小さくするような a, b の値を求める。
■ データの準備
「データ表」ワークシート全体を選択し、新規ワークシート「数量データ」に複写する。
複写したデータのうち、質的データ(性別、声喩、慣用句など)を削除し、数量データのみを残す。
| データ | データ数(N) | 名詞率との相関係数 |
|---|---|---|
| (1)全体データ | 2472 | 0.721 |
| (2)漢字率25%未満のデータ | ||
| (3)漢字率45%以上のデータ | ||
| (4)漢字率30%以上35%未満のデータ | ||
| (2)と(4)を併せたデータ |