[６]　母集団と標本

[6.1]　標本抽出

　推測統計　…　母集団からとられた比較的小さな標本を手がかりとして母集団のあるべき姿を推測する。
　　　　　　　　標本に基づいて計算された量（統計量）から、母集団の数理的特性（母数）を推定する。

6.1.1 標本抽出の方法

　ランダムサンプリング　…　母集団の中の要素を、すべての要素が等しい確率で、無作為に抽出する。
　層化無作為抽出法　…　母集団を予めいくつかの層に分け、その層の中で無作為抽出する。

6.1.2 標本抽出分布

　標本抽出分布　…　ある母集団から、特定サイズの標本の抽出を繰り返したときに、それらの標本から得られる統計量（平均など）の分布。

• 理論的標本抽出分布の平均は、母平均と同じ。
  　　⇒　標本抽出を多数繰り返すと、標本抽出分布の平均値や標準偏差は理論値に近づく。
• 理論的標本抽出分布の標準偏差（標準誤差）は、
　　　理論的標準誤差 ＝ 母標準偏差 ／√標本サイズ
　　⇒　標準誤差は、標本サイズｎが大きくなるほど、小さくなる。


• 母標準偏差σが不明のとき、標本標準偏差を代用して、標準誤差を推定する。
　　　　　推定標準誤差 　＝　標本標準偏差 ／ √標本サイズ

　標本抽出分布と正規性（無作為抽出の場合）

• 母集団分布が正規であれば、平均値の標本抽出分布も正規分布となる。
• 母集団が正規分布でなくても、標本サイズが大きくなる と、平均値の標本抽出分布は正規分布に近づく。（中心極限定理）

[6.2]　乱数とサンプリング

■ 乱数の発生：rand()
関数 rand() は０以上１未満の小数をランダムに生成する。
１以上ｘ未満にある範囲の乱数を生成するには、（　　　　　　　　　　　　）を実行する。
計算式を複写して、必要数だけのデータを取る。

■ ランダムサンプリング
ある母集団（p.96, 図7-1）のデータ(population.dat)を新ブックに読み込む。
「ツール」メニューの「分析ツール」から「サンプリング」を選択。
「入力元」としてA列を選択。「ランダム標本数」として500を指定。
「出力先」を新規ワークシート（「抽出ｎ=500」）に指定して、OKを押す。
 　標本サイズ、抽出回数を変えて、標本抽出を繰り返す。
「分析ツール」→「基本統計量」でデータの平均、標準偏差の値の変化を調べる。

[6.3]　標本抽出シミュレーション

　AWK というプログラミング言語を使って、標本抽出をシミュレーションしてみよう。 　

■ 検証する内容
標本抽出のシミュレーションを行って、次の内容を確認します。
(1) 抽出回数を多くすると、標本平均値の平均値は母平均に近づく。
(2) 抽出標本の平均値の標準偏差（標準誤差）は、標本サイズが大きくなるほど、小さくなる。

■ データを準備する
 次のファイルsampling.zipをダウンロードして、解凍する。
解凍してできたフォルダ（sampling）を、適当な場所(H:\sampling)に移動する。
samplingフォルダには、次のファイルが含まれている。

プログラムファイル	awk.exe（AWKスクリプトを実行するプログラム） sampling.awk（標本抽出シミュレーション用AWKスクリプト） sampling.bat（標本抽出を行うバッチプログラム） central.bat（中心極限定理用バッチプログラム
データファイル	basic.dat（基本語彙率データ） past.dat（過去形率データ） katakana.dat（カタカタ語使用回数データ） slength.dat（文長データ） age.dat（年齢データ）

■ コマンドプロンプトを起動する
「スタート」→「プログラム」→「アクセサリ」→「コマンドプロンプト」を選択。
 黒い画面で、h: と入力し、「Enter」キーを押して、コマンドを実行する。
 次に、cd sampling と入力し、実行。（コマンドcd は、指定されたディレクトリへの移動）

■ シミュレーションの実行
 sampling 5 2 と入力し、実行する。（標本サイズ 5、繰り返し回数 2 を指定）
 画面に母集団の特性（母数）や無作為抽出の結果（標本抽出分布の平均値および標準誤差）が表示される。
 結果データ（標本サイズ、抽出回数、標本抽出分布の平均、母平均との絶対差、標準誤差）をExcel に記録しておく。（注：絶対値計算は、=abs(値）を使う。）
 標本サイズや抽出回数を変えて、シミュレーションを繰り返す。

標　本 サイズ	抽　出 回　数	抽出分 布平均	母平均 との差	標　準 誤　差	標　本 サイズ	抽　出 回　数	抽出分 布平均	母平均 との差	標　準 誤　差
5	2				2	20
5	3				3	20
5	4				4	20
5	5				5	20
5	10				10	20
5	20				20	20
5	30				30	20
5	50				50	20
5	100				100	20
5	200				200	20
5	500				500	20

[課題]
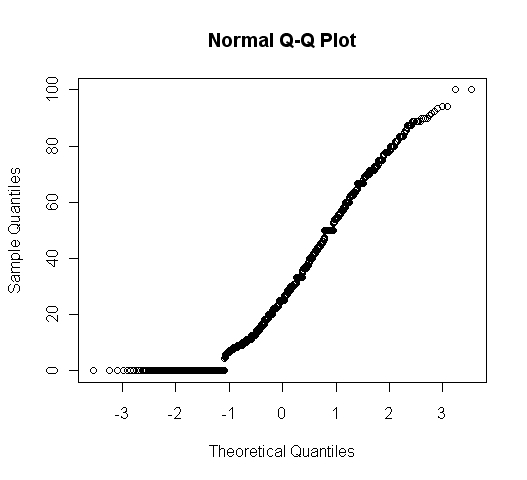
　下の図１は、朝日新聞98年の投書の文末過去形率のヒストグラム、図２は文末過去形率の正規確率プロットである。

図１と図２から、このデータが正規分布をしていないことが確認できる。
　中心極限定理は、「標本サイズが大きくなると、母集団が正規でなくても、標本抽出分布は正規分布に近づいていく」と予測する。そこで、正規分布とは言えない過去形率データ(past.dat)を母集団として、標本抽出をおこない、この原理の妥当性を調べてみよう。
1. 標本サイズを1, 2, 3, 5, 10, 100, 500に設定し、それぞれ50個の標本を抽出しなさい。
　例：central 2 20 （各標本の平均値は n2.out という名前のファイルに保存されている。）
2. n2.out などを Excel で開き、得られたデータの正規性を調べる。（前回参照のこと）
　正規性の目安として、得られたデータと対応する正規確率との相関係数を計算する。相関係数が１に近いほど、正規性が高いと判断できる。
3．標本サイズと相関係数の変化を記録し、折れ線グラフに描いて、正規分布に近づくかどうかを判断しなさい。

標本サイズ(n)	<抽出回数	抽出データ名	相関係数(r)
1	20	n1.out
2	20	n2.out
3	20	n3.out
4	20	n4.out
5	20	n5.out
10	20	n10.out
100	20	n100.out
500	20	n500.out

3. 標本サイズをＸ軸、相関係数データをＹ軸にとって、両者の関係を折れ線グラフで表示する。
4. グラフから、中心極限定理の予測が当てはまっているかどうかを検証しなさい。