[10] χ２乗検定

　度数データを対象とし、一定のカテゴリーに分けられた変数間に差異があるかどうかを、χ² 値を用いて検定する。χ² 値は、観測度数と期待度数のずれの大きさを表す統計量で、χ² 分布に従う。

[10.1]　適合度の検定

　相互に独立した k 個のカテゴリーに振り分けられた観測度数 O₁, O₂,..., O_k が、理論的期待度数 E₁, E₂, ..., E_k と一致しているかどうかを、χ² 統計量を用いて検定する。

手順

1. 帰無仮説：各カテゴリーの度数は、対応する期待度数に等しいと仮定
   　　対立仮説：カテゴリーの１つまたはそれ以上に関し、比率が等しくない。
   
2. 有意水準と臨界値：設定した有意水準と自由度でのχ² 値をχ² 分布表から読み取り、臨界値とする。
   　　　自由度 df ＝ カテゴリー数 − 1
   　算出されたχ² 値が臨界値以上なら帰無仮説を棄却する。それ以外は帰無仮説を採択する。
   
3. 検定量の算出：
   　　　χ² ＝ �倍(O_j−E_j)² / E_j}
   　※１：χ² 値は、期待度数からの観測度数の隔たりの大きさを表す。
   　※２：イエーツの修正…自由度が１で、どれかの E_j が 10 以下の時
   　　　　χ² ＝�倍(|O_j−E_j| − 0.5)² / E_j}
   
4. 結論：
   

[10.2]　独立性の検定

　N個の標本が、AとBの変数に関して分類されたとき、２つの変数が独立しているかどうかを、χ² 統計量を用いて検定する。

手順

1. 分割表の作成：
   　(1) 全データを、独立性を吟味する２つの変数のサブカテゴリへ振り分ける。
   　(2) 各サブカテゴリおよび全体の計（周辺度数）を求める。
   　(3) 各セルの期待度数を算出する。
   　　　　E_ij ＝ （i 行の周辺度数）×（j 列の周辺度数）／サンプルサイズ（N)
   
2. 帰無仮説：２つの変数は独立している。
   対立仮説：独立とは言えない。２つの変数は関連がある。
   
3. 有意水準と臨界値：設定した有意水準と自由度でのχ² 値をχ² 分布表から読み取り、臨界値とする。
   　　　自由度 df …i 行 j 列の分割表なら、df ＝ (i - 1)(j - 1)
   　算出されたχ² 値が臨界値以上なら帰無仮説を棄却する。それ以外は帰無仮説を採択する。
   
4. 検定量の算出：
   　　　χ²0 ＝ �倍(O_j−E_j)² / E_j}
   　　　※１：2 × 2 の分割表で、どこかの E_ij が 10 以下なら、イエーツの修正を行う。
   
5. 結論：

クラメールの連関係数とコーエンの実際効果量
　χ² 検定が有意であれば、クラメール(Cramer)の連関係数を算出する。クラメールの連関係数は c × k 分割表における２変数の相関の強さを表す係数である。
　　　  V ＝ sqrt( χ² / N( min - 1 ) )
　　　　 ※ N はデータ数、min は行数と列数のうち、小さいほうの値。
　V の値は、完全に独立であれば 0、完全に関連すれば 1 となる。

実際問題として結果が意味があるかどうか、効果の大きさを判断するには、コーエンのw^統計量を用いる。
　　　w^ = sqrt( χ² / N )
効果量wの値は次の目安によって解釈される。(Kirk 20082: 475)

w^の値	効果量の解釈
0.1〜0.3	小さい(small)
0.3〜0.5	中くらい(medium)
0.5以上	大きい(large)

標準化残差の分析 　カイ２乗検定の結果が有意であるとき、各セルの調整済残差(adjusted residual)を分析することで、当てはまりの悪いセルを特定することができる。
　残差：観測値n_ij−期待値_ij。
　調整済残差d_ij＝残差_ij／残差の標準偏差SE(残差_ij)
　　　　　　　　＝（観測値n_ij−期待値_ij）／sqrt(期待値_ij*(1-当該セルの行割合p_i+)*(1-当該セルの列割合p_+j））
　　調整済残差は、独立性の仮定の下で、標準正規分布N(0, 1²)に近似的に従う。すなわち、絶対値が２または３以上であれば、当該セルの当てはまりが悪いと言える。(Agresti 1990, p.81)

[10.3]　比率の等質性の検定

　ある標本を一定の基準で下位カテゴリに分けた場合の比率と、別の標本での比率が等しいかどうかを、χ² 値を用いて検定する。

手順
　独立性の検定の場合と同じ。

[10.4]　投書データの独立性検定

　新聞投書データの中の任意の２つの（カテゴリ）変数が独立しているかどうかを検定してみよう。たとえば、性別と引用率について独立性検定を行う。

手順

1. 引用率データを質的データへ変換
   ・datahyou.xls から、引用率データと性別データを新規ブックにコピーアンドペーストする。
   ・引用率（数量データ）を「引用率カテゴリ」データに変換する。
   ・引用率（A列）が5%未満なら「少ない」、10%未満なら「普通」、10%以上なら「多い」と分類する。
   ・if 関数：数値条件に応じてカテゴリに分類したい
   　=if(条件, "合致したときのカテゴリ名", "合致しないときのカテゴリ名")
   　３つ以上のカテゴリに分けたいとき→if条件の埋め込み
   　=if(条件1, "合致したときのカテゴリ名1", if(条件2, "合致したときのカテゴリ名2", "合致しないときのカテゴリ名3") )
2. 分割表の作成
   ・「データ」→「ピボットテーブル　レポート」を選択
   ・行と列にカテゴリ変数を指定し、「データ」に度数集計したい変数を指定する。
   
   
   
   
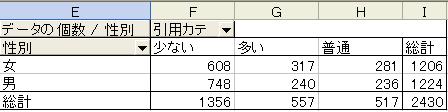
3. 検定量χ²₀ を計算する
   ・Excel「分析ツール」には「χ² 検定」がない！
   ・公式に従い、表計算を行う
   (1)期待度数表を作成：ピボットテープルをコピーし、表周辺の計以外の数値を再計算。
   (2)χ²₀ を表計算
4. 臨界値または上側確率を求める
   ・=chiinv( α, df )：有意水準α、自由度 df に対応するχ² （臨界値）を 返す
   ・=chidist( χ², df )：χ² 分布において χ²₀ 以上の値が得られる確率（上側確率）を返す
・検定量と臨界値を比較して（または上側確率から判断して）、結論を出す。 　
5. 検定結果が有意の場合、調整済残差を算出して、当てはまりの悪いセルを特定する。
6. 検定結果が有意の場合、クラメールの連関係数を算出して報告する。コーエンのw^統計量を算出して、実際的効果を判断する。