[５]　正規分布と標準化

[5.1] 正規分布

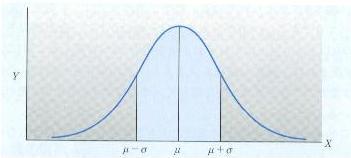
　多くの測定値を整理すると、平均付近の値が多く極端に大きい値や極端に小さい値は少ない。
　　⇒西洋の釣鐘を伏せた形状に分布する。
　無限数のケースを測定すると、正規分布Ｎ（μ，σ²）を なす。
　正規分布の特徴：
　　・平均値を境に、左右均斉（平均値、中央値、最頻値が同じ値）。 　　
　　・左右の裾野は、平均値から離れるほどＸ軸に近づいていく。 　
　　・平均値μと標準偏差σの値から、データ全体の分布の様子が分かる。
　　　μ±σの範囲に全データの約68％、μ±２σの範囲には約95％が含まれる。
　　　⇒推測統計で利用される。

[5.2] 相対的位置の測度

　全体のデータの中で、個々のデータが占める位置を示す測度。

5.2.1 Ｚ得点と偏差値

　標準化：正規分布を、標準正規分布へｚ変換すること。
　　　 z = （ X - μ ）/ σ
　　　z の分布は、標準正規分布Ｎ（０，１²）（平均値０、標準偏差１）となる。
　　　⇒ｚの値が決まれば、分布グラフ上の面積（確率）が求められる。
　　　　例：ｚ>=1.96 の面積は 0.025 ⇒ 全体の95％は -1.96 <= z <= 1.96 の範囲内。

　偏差値：ｚ得点を、平均50、標準偏差10の分布に変換。 　　　
　　　Ｚ = 10 * z + 50

5.2.2 パーセンタイル順位・点

　パーセンタイル順位：ある１つの得点の下に入る得点の数の百 分率。
　　例：80％順位は、その下に80％、その上に20％が入る。
　パーセンタイル点：特定のパーセンタイル順位に対応するデータの 値。

[5.3] 標準化と正規性

5.3.1 Ｚ得点と偏差値を求める

　新聞投書データの中から基本語彙率に関して、各データの相対的位置（z得点と偏差値）を求めてみよう。

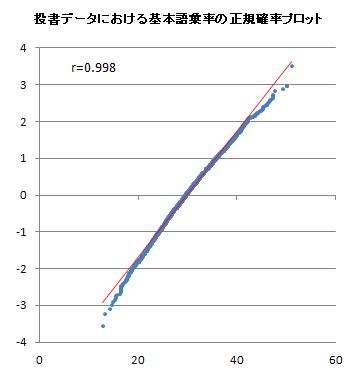
5.3.2 分布の正規性：正規確率プロット

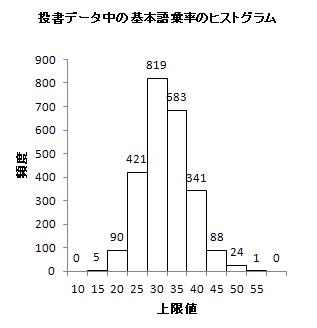
基本語彙率データのヒストグラムを描くと、正規分布に近い分布の様子が見てとれます。

基本語彙率データの正規確率プロットを描き、分布の正規性を調べてみよう。