| [7.1] 統計的仮説検定の考え方 |
| [7.2] 統計的検定の手順 |
| [7.3] 第1種と第2種の誤り |
| [7.4] 平均値の区間推定 |
| [7.5] 母比率の検定と推定 |
標本での変数間の「差や関連性」に基づいて、母集団での「差や関連性」を予測する
→母集団においても「差や関連性」が本当に(有意に)あると判断できるかを決定する。
標本に見られる差異や関連性が、母集団においても有意な差や関連性と認められるか、どうかを決定する。
偶然(=要素の抽出)による誤差程度の差なのか、意味のある、実質的なものなのか?
母集団と標本抽出分布の間の統計数理的(確率)な関係に基づいて、「客観的」に判断する。
帰無仮説 H0:母集団の値と標本の値には、差がない。(通常、研究者が否定したい仮説)
X~ - μ = 0
対立仮説 H1:帰無仮説を否定する形式の仮説。(=研究者が主張したい仮説)
検定の方向性:
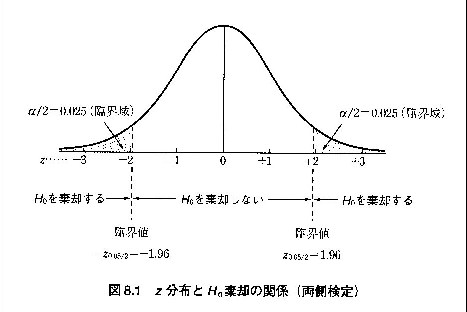
(i) X~ - μ ≠ 0 (X~>μ か X~<μ かは推測できない → 両側検定)
(ii) X~ - μ < 0 (X~>μ と考える根拠あり → 右片側検定)
(iii) X~ - μ > 0 (X~<μ と考える根拠あり → 左片側検定)
有意水準 α:帰無仮説を棄却するかどうかを決める、境界的な確率の値。
慣例的にα= 0.05, 0.01 などに設定することが多い。
決定のルール:検定量が棄却域に入るなら帰無仮説を棄却する。そう
でないなら帰無仮説を採択する。
目的や条件(標本サイズの大きさ、母分散が未知など)に応じて、検定量 z, t, F, χ2を決める。
標本の平均値が母平均と異なるか?
ケース1:σが既知なら、この標本平均値 X~ のz検定量
z0を求める。
z0 = (X~-μ) / σ/√n
⇒ zは標準正規分布に従う。
ケース2:σが未知なら、標本標準偏差 S
で代用して、この標本平均値の t 検定量 t0 を求める。
t0 = (X~-μ) / S/√n
⇒ t は自由度 n - 1 の t 分布に従う。
第1種の誤り:本当は真であるH0を
誤って棄却する危険率。有意水準αに等しい。
第2種の誤り:本当は偽であるH0を誤って棄
却しない確率β。
2種類の誤りは、一方を小さくしようとすると他方が必ず大きくなり、両方を同時に小さくすることはできない。
検出力:偽であるH0を正しく棄却する確率
で、1−βに等しい。

検出力を高めるには、
標本の平均値X~に基づいて、母平均μの範囲を推定する。
平均μの母集団から、標本サイズNで標本抽出するときの分布の平均はX~=μ、標準偏差(標準誤差SE)はσ/√Nの正規分布となる。今、σが未知なので標本標準偏差Sで代用すると、標本抽出分布はt分布となる。このt分布の平均はX~=μ、標準偏差はS/√n、自由度n−1 のt分布となる。
このt分布の95%信頼区間(あるいは99%信頼区間)を計算する。
下限値:X~−tα/2, df * S/√N
上限値:X~ + tα/2, df * S/√n
(注意:Excelでtα/2, dfを求めるとき、tinv(0.05, df)またはtinv(0.01, df)とする。αの値を2で割らない。)
標本で得られた割合に基づいて、信頼係数95%(あるいは99%で)母集団での割合を推定することができます。標本サイズが30以上のときは、標準正規分布を利用して、信頼区間を求めます。pは標本割合、nは標本サイズとすると、
下限値:p - zα/2 * sqrt( p * ( 1-p ) / n )
上限値:p + zα/2 * sqrt( p * ( 1-p ) / n )